
Wil je in je scriptieonderzoek onderzoeken hoe verschillende factoren elkaar beïnvloeden? Regressieanalyse is een statistische techniek waarmee je relaties tussen variabelen kunt analyseren en voorspellingen kunt doen. Of je nu werkt aan een bachelor- of masterthesis, deze gids helpt je stap voor stap bij het uitvoeren van een correcte analyse.
In dit artikel lees je:
- Wat is een regressie analyse en wanneer gebruik je deze methode
- Welke soorten regressieanalyse er zijn (enkelvoudige en meervoudige)
- Hoe je regressieanalyse uitvoert in SPSS met praktische voorbeelden
- Welke assumpties je moet controleren voor betrouwbare resultaten
- Wanneer uitbesteden scriptie-analyse zinvol kan zijn.
Wat is een regressieanalyse?
Regressieanalyse is een statistische techniek waarmee je verbanden tussen variabelen onderzoekt. Je analyseert hoe één of meerdere onafhankelijke variabelen (X) een afhankelijke variabele (Y) beïnvloeden. Deze methode helpt je patronen te ontdekken, effecten te meten en voorspellingen te doen op basis van je dataset. De term regressie werd geïntroduceerd door de Engelse antropoloog Francis Galton.
Wij nemen snel contact met je op.

Wanneer kies je voor regressieanalyse in je scriptieonderzoek?
Regressieanalyse is geschikt wanneer je causale verbanden tussen variabelen wilt onderzoeken in kwantitatief onderzoek. Je gebruikt deze statistische methode specifiek wanneer je wilt analyseren hoe onafhankelijke variabelen een afhankelijke variabele beïnvloeden. Deze techniek werkt met continue data op interval of ratio meetniveau.
Je kiest voor regressieanalyse wanneer:
Twijfel je of regressieanalyse de juiste methode is voor jouw onderzoek? SPSS hulp en begeleiding bij je scriptie kan je ondersteunen bij het maken van de juiste methodologische keuzes en het correct uitvoeren van de analyse.
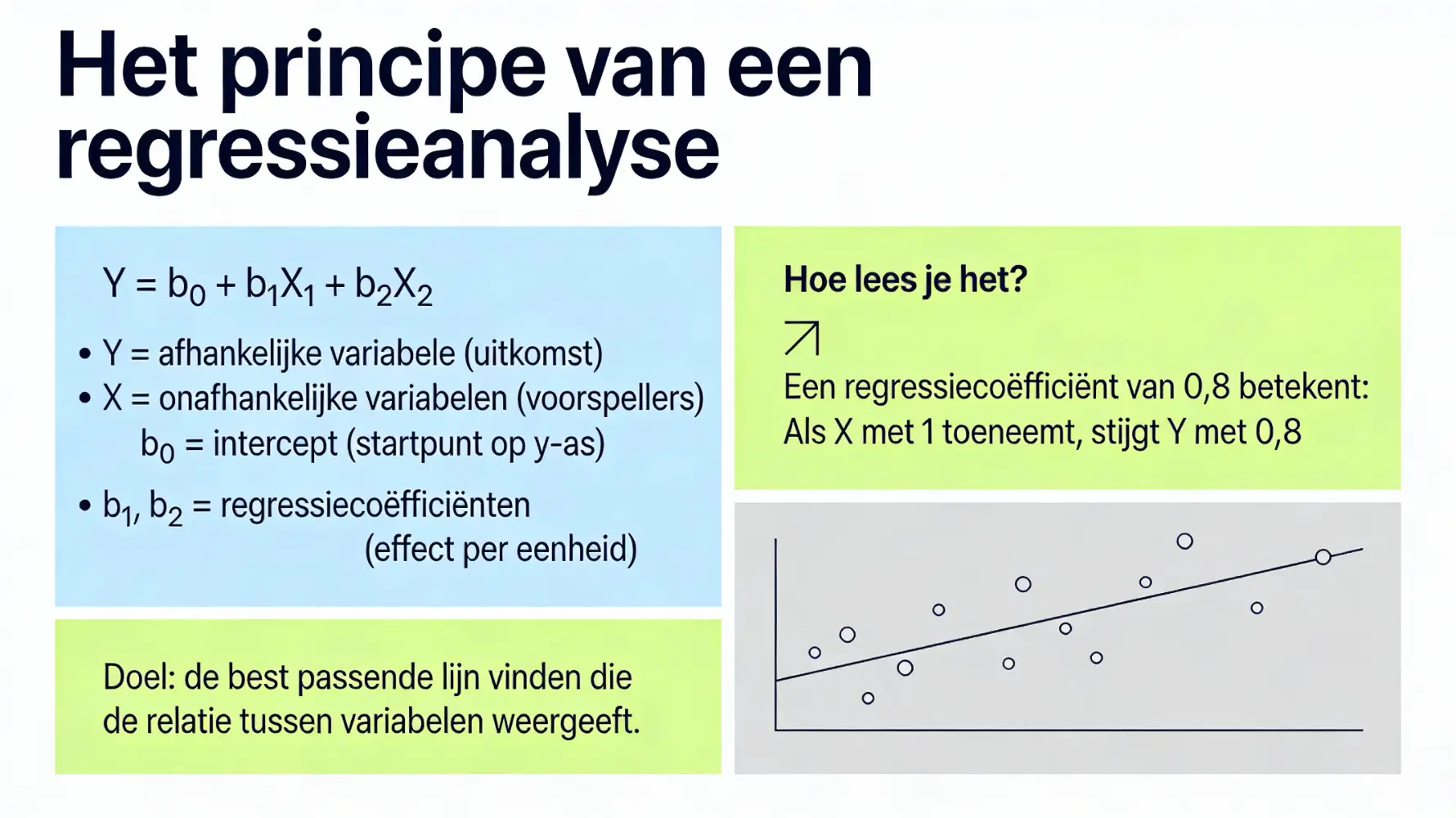
Het principe van een regressieanalyse
Het kernprincipe van regressieanalyse is het opstellen van een wiskundige vergelijking die de relatie tussen variabelen beschrijft. Deze regressievergelijking wordt uitgedrukt in een lineaire functie die voorspellingen mogelijk maakt.
De basisformule ziet er als volgt uit:
Y = b₀ + b₁X₁ + b₂X₂ + … + bₚXₚ
Waarin:
- Y = de afhankelijke variabele die je wilt verklaren of voorspellen
- X₁, X₂, …, Xₚ = de onafhankelijke variabelen (ook wel verklarende variabelen of predictoren genoemd)
- b₀, b₁, …, bₚ = de regressiecoëfficiënten die de sterkte en richting van het effect aangeven
De regressiecoëfficiënt geeft aan hoeveel de afhankelijke variabele verandert wanneer de onafhankelijke variabele met één eenheid toeneemt, terwijl alle andere variabelen gelijk blijven. Het getal b₀ is het intercept: de geschatte waarde van Y wanneer alle onafhankelijke variabelen nul zijn.
In wiskundige termen herken je hier de vertrouwde lineaire functie uit je middelbareschooltijd: f(x) = y. Je berekent de y-waarde door een waarde voor x in te vullen. Bij regressieanalyse zoek je de best passende lijn door een wolk van datapunten. Deze regressielijn minimalisert de afstand tussen de voorspelde en werkelijke waarden van de afhankelijke variabele, waardoor je de meest nauwkeurige voorspellingen kunt doen op basis van je dataset.
Belangrijke begrippen bij regressieanalyse
Om een regressieanalyse correct uit te voeren en te interpreteren, moet je vertrouwd zijn met een aantal kernbegrippen uit de statistiek. Deze terminologie komt je tegen in de output van statistische programma’s zoals SPSS en bij het rapporteren van je resultaten. Hieronder vind je een overzicht van de essentiële begrippen die je regelmatig tegenkomt.
| Begriff | Uitleg |
|---|---|
| Onafhankelijke en afhankelijke variabele | De onafhankelijke variabele (X) is de verklarende factor waarvan je vermoedt dat deze invloed heeft. De afhankelijke variabele (Y) is de uitkomst die je wilt voorspellen of verklaren. |
| Regressielijn en intercept | De regressielijn is de best passende lijn door je datapunten. Het intercept (b₀) is het punt waar deze lijn de y-as snijdt – de geschatte waarde van Y wanneer alle onafhankelijke variabelen nul zijn. |
| Regressiecoëfficiënten (b-waarden) | Deze coëfficiënten geven aan hoeveel de afhankelijke variabele verandert per eenheid toename van een bepaalde onafhankelijke variabele, terwijl andere variabelen constant blijven. |
| Residuen | Het verschil tussen de werkelijke en voorspelde waarde. Residuen van het model laten zien hoe goed je model de data voorspelt. |
| Verklaarde variantie (R²) | Een statistiek tussen 0 en 1 die aangeeft hoeveel variatie in de afhankelijke variabele verklaard wordt door het regressiemodel. Een hogere R² betekent een beter model. |
Heb je moeite met het berekenen of interpreteren van deze statistieken? STATA Hulp kan je ondersteunen bij complexe analyses.
Soorten regressieanalyse
Er bestaan verschillende soorten regressieanalyse, elk geschikt voor specifieke onderzoekssituaties. De keuze voor een bepaald type hangt af van het aantal onafhankelijke variabelen in het model en het meetniveau van je afhankelijke variabele. Hieronder bespreken we de drie belangrijkste vormen die je in scriptieonderzoek tegenkomt.
Enkelvoudige lineaire regressie
Enkelvoudige lineaire regressie is de eenvoudigste vorm waarbij je de relatie tussen twee variabelen onderzoekt: één onafhankelijke variabele en één afhankelijke variabele. Deze lineaire regressie analyse gebruikt je wanneer je wilt onderzoeken hoe één specifieke factor een uitkomst beïnvloedt. Bijvoorbeeld: het effect van studieuren op tentamencijfers. Het resultaat is een rechte lijn die de samenhang tussen beide variabelen weergeeft.
Meervoudige lineaire regressie
Bij meervoudige regressie (ook wel multipele regressie genoemd) analyseer je het effect van meerdere onafhankelijke variabelen tegelijk op één afhankelijke variabele. Deze meervoudige regressie analyse is krachtiger omdat je kunt controleren voor verstorende factoren. Je kunt bijvoorbeeld het tentamencijfer verklaren aan de hand van zowel studieuren, voorkennis als motivatie. Zo ontdek je welke variabelen het meest significant zijn.
Logistische regressie in het kort
Logistische regressie analyse gebruik je wanneer je afhankelijke variabele categorisch is (bijvoorbeeld wel/niet geslaagd). In tegenstelling tot lineaire enkelvoudige of meervoudige methoden, voorspelt deze techniek de kans op een bepaalde uitkomst. Deze variant valt buiten de scope van dit artikel over lineaire regressie.
Assumpties bij regressieanalyse
Voor betrouwbare resultaten moet je regressiemodel aan bepaalde statistische voorwaarden voldoen. Deze assumpties regressie analyse zijn essentieel om te controleren voordat je je bevindingen interpreteert. Als deze aannames geschonden worden, kunnen je conclusies onbetrouwbaar zijn.
Lineariteit
De relatie tussen de onafhankelijke en afhankelijke variabele moet lineair zijn. Controleer dit met een spreidingsdiagram. Als het patroon gebogen is, voldoet je data niet aan deze assumptie.
Normaliteit van residuen
De residuen van het model moeten normaal verdeeld zijn, vooral bij kleine steekproeven. Controleer dit met een histogram of Q-Q plot. Afwijkingen maken significantietoetsen onbetrouwbaar.
Homoscedasticiteit
De spreiding van residuen moet constant blijven over alle waarden van de onafhankelijke variabele. Schendingen leiden tot onbetrouwbare standaardfouten en incorrecte significantietoetsen. Controleer dit met een plot van residuen tegen voorspelde waarden.
Onafhankelijkheid van waarnemingen
Elke observatie in je dataset moet onafhankelijk zijn. Deze assumptie wordt geschonden bij herhaalde metingen of geclusterde data. Dit leidt tot onderschatte standaardfouten en te snel significante resultaten.
Het controleren van deze assumpties doe je in programma’s zoals SPSS via diagnostische plots en toetsen.
Stappenplan regressieanalyse uitvoeren
Het uitvoeren van een regressieanalyse vereist een systematische aanpak om betrouwbare resultaten te garanderen. Volg dit stappenplan om je analyse correct door te voeren, van het formuleren van je onderzoeksvraag tot het interpreteren van de output.
Stap 1: Onderzoeksvraag en hypothesen formuleren
Begin met een heldere onderzoeksvraag die de relatie tussen één afhankelijke en één of meerdere onafhankelijke variabelen specificeert. Formuleer concrete hypothesen over de verwachte verbanden tussen de variabelen. Bijvoorbeeld: “In hoeverre voorspelt het aantal studieuren het tentamencijfer?” Bepaal ook of je een enkelvoudige regressieanalyse (één predictor) of meervoudige regressie (meerdere predictoren) nodig hebt.
Stap 2: Data verzamelen en voorbereiden
Verzamel je dataset en controleer de kwaliteit van je gegevens. Verwijder ontbrekende waarden, identificeer uitschieters en controleer of je variabelen het juiste meetniveau hebben (interval of ratio voor lineaire regressie). Deze stap van analyseren van gegevens is cruciaal voor betrouwbare resultaten.
Stap 3: Regressieanalyse draaien in SPSS of Excel
Voer de analyse uit in je gekozen statistisch programma. In SPSS ga je naar Analyze → Regression → Linear. Selecteer je afhankelijke variabele en voeg de onafhankelijke variabelen toe. Het programma berekent automatisch de regressiecoëfficiënten en produceert verschillende tabellen met resultaten.
Stap 4: Assumpties controleren
Controleer of je data voldoet aan de assumpties voor lineaire regressie: lineariteit, normaliteit van residuen, homoscedasticiteit en onafhankelijkheid. Gebruik diagnostische plots en toetsen om dit te verifiëren. Deze stap bepaalt of je resultaten geldig zijn.
Stap 5: Resultaten interpreteren en rapporteren
Analyseer de output van een regressieanalyse door te kijken naar de R², regressiecoëfficiënten en significantieniveaus in de tabel. De ANOVA-tabel (Analysis of Variance) toont of het model een significante verbetering biedt ten opzichte van het gemiddelde. Interpreteer welke variabelen significant bijdragen en rapporteer je bevindingen helder in je scriptie.
Voorbeeld van een regressieanalyse
Om het principe van regressieanalyse concreet te maken, werken we een praktijkvoorbeeld uit. Dit voorbeeld laat zien hoe je stap voor stap van onderzoeksvraag naar conclusie komt bij een enkelvoudige lineaire regressie.
Casus: Voorspellen van studieresultaten
Een opleiding wil tijdig achterblijvende studieresultaten kunnen signaleren. Bij een toelatingsonderzoek worden cijfers geregistreerd die een steekproef van aankomende studenten halen op een wiskundetoets. Binnen twee jaar wordt bekeken wat de geregistreerde studieresultaten per student zijn. De opleiding wil achtergaan per student weten of de wiskundetoets vooraf van elke student iets zegt over te verwachten studieresultaten.
Op het bureau van de studiebegeleider ligt een dossier van een student met een testresultaat van x = 50.
Onderzoeksvraag: Wat is het te verwachten studieresultaat (y) van deze student uitgedrukt in een cijfer?
Stap 1: Data verzamelen
De dataset bevat wiskundetoetsscores (onafhankelijke variabele X) en daadwerkelijke studieresultaten na twee jaar (afhankelijke variabele Y) van eerdere studenten. Deze variabelen zijn beide op interval meetniveau gemeten, wat geschikt is voor lineaire regressie.
Stap 2: Regressieanalyse uitvoeren
Door de regressieanalyse in SPSS uit te voeren, vinden we de volgende regressievergelijking:
Y = 20 + 0,8X
Hierbij is:
- Y = voorspeld studieresultaat
- X = wiskundetoetsscore
- 20 = intercept (b₀)
- 0,8 = regressiecoëfficiënt (b₁)
Stap 3: Voorspelling berekenen
Voor de student met x = 50 berekenen we:
Y = 20 + 0,8(50) = 20 + 40 = 60
Interpretatie: Op basis van de wiskundetoetsscore van 50 voorspelt het model dat deze student een studieresultaat van 60 zal behalen.
Stap 4: Resultaten interpreteren
De regressiecoëfficiënt van 0,8 betekent dat per punt toename op de wiskundetoets, het voorspelde studieresultaat met 0,8 punt stijgt. De ANOVA-tabel toont dat het model een significante verbetering biedt (p < 0,05), wat aangeeft dat de wiskundetoets een betekenisvolle voorspeller is.
Dit voorbeeld demonstreert hoe regressieanalyse wordt gebruikt om concrete voorspellingen te doen die de opleiding kan gebruiken voor vroege interventies bij studenten.

Checklijst voor regressieanalyse in je scriptie
Voordat je de resultaten van je regressieanalyse interpreteren en rapporteren in je scriptie, doorloop deze checklijst. Zo voorkom je veelgemaakte fouten en zorg je ervoor dat je analyse methodologisch correct is uitgevoerd.
Checklijst regressieanalyse:
Heb je hulp nodig bij het analyseren van je scriptie?
Loop je vast bij het uitvoeren of interpreteren van je regressieanalyse? Onze ervaren ghostwriters helpen je met het analyseren van gegevens, het correct toepassen van statistische technieken in SPSS, het controleren van assumpties en het rapporteren van resultaten. We ondersteunen je bij verschillende variabelen en complexe analyses, zodat je scriptie methodologisch solide is.
FAQ
Wat is het verschil tussen regressie en correlatie?
Hoe bepaal ik of mijn onderzoek geschikt is voor regressieanalyse?
Je onderzoek is geschikt voor regressieanalyse wanneer je een causale relatie tussen variabelen wilt onderzoeken met kwantitatieve data. De afhankelijke variabele moet op interval of ratio meetniveau zijn. Je hebt een duidelijke onderzoeksvraag waarbij je wilt weten hoe één of meerdere onafhankelijke variabelen een uitkomst beïnvloeden. Bij categorische afhankelijke variabelen (bijvoorbeeld ja/nee) gebruik je logistische regressie in plaats van lineaire regressie.
Welke assumpties moet ik controleren bij regressieanalyse?
Je moet vier belangrijke assumpties controleren: (1) Lineariteit – de relatie tussen onafhankelijke en afhankelijke variabele moet lineair zijn, (2) Normaliteit – de residuen van het model moeten normaal verdeeld zijn, (3) Homoscedasticiteit – de spreiding van residuen moet constant blijven over alle waarden van de onafhankelijke variabele, en (4) Onafhankelijkheid – waarnemingen mogen niet gecorreleerd zijn. Je controleert deze via diagnostische plots in SPSS.
Hoeveel respondenten heb ik nodig voor een betrouwbare regressieanalyse?
Als vuistregel geldt minimaal 15-20 observaties per onafhankelijke variabele in je regressiemodel. Voor enkelvoudige regressie met één predictor is een steekproef van minimaal 30 respondenten aan te raden. Bij meervoudige regressie met meerdere onafhankelijke variabelen heb je een grotere dataset nodig. Een steekproef van 100+ observaties geeft over het algemeen stabielere en betrouwbaardere resultaten, vooral wanneer je verschillende variabelen tegelijk analyseert.
- Wat is een regressieanalyse?
- Wanneer kies je voor regressieanalyse in je scriptieonderzoek?
- Het principe van een regressieanalyse
- Belangrijke begrippen bij regressieanalyse
- Soorten regressieanalyse
- Assumpties bij regressieanalyse
- Stappenplan regressieanalyse uitvoeren
- Voorbeeld van een regressieanalyse
- Checklijst voor regressieanalyse in je scriptie
- Heb je hulp nodig bij het analyseren van je scriptie?
- FAQ
- Professionele hulp bij je studie en scriptie
Populaire artikelen
Professionele hulp bij je studie en scriptie
Een intakegesprek is altijd geheel vrijblijvend, we geven je graag meer persoonlijke informatie en een advies op maat, zodat je vooraf een goed beeld hebt bij wat we voor jou kunnen betekenen.

















